Description des condensateurs.

page 3/3

• Le Nécessaire

  • Le condensateur s'oppose aux variations "rapides" de la  tension à ses bornes (on désignera cette tension Vc).

  • Que signifie "rapide" ?
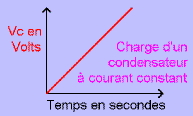
    Rapide signifie que le temps intervient, on se souvient alors de l'exemple du ballon qui se gonflait petit à petit avec de l'eau. Pour le condensateur, c'est la même chose: le passage immédiat de Vc de 3V à 8V est impossible, le condensateur met un temps à se charger.

  • Nous avons vu précédemment que: Vc = Q/C  or Q = I.t  d'où  Vc = ( I.t )/C    avec I courant de charge constant (en Ampère),
    Q charge du condensateur (en Coulomb), C capacité du condensateur (en farad) et t le temps (en seconde).
    La tension est donc bien fonction du temps.

  • Cependant, le courant de charge du condensateur n'est pas toujours constant. Nous allons donc étudier le cas d'un circuit RC.

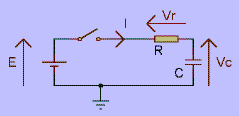
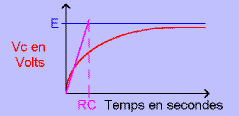
    Commençons par analyser le schéma. Le montage est constitué d'un générateur de tension, un interrupteur, une résistance et un condensateur. Le condensateur est supposé déchargé, on ferme l'interrupteur à t=0, le condensateur se charge, Vc augmente jusqu'à atteindre la valeur E. Mais le courant n'est pas constant, on utilise alors la formule:                        Vc(t) = Vc(infini) + [ Vc(0) - Vc(infini) ].exp(-t/RC)

                     Avec Vc(t) la tension aux bornes du condensateur à l'instant t, Vc(infini) la tension Vc très longtemps après avoir fermé l'inter (E dans ce cas), Vc(0) la tension Vc à t=0, le temps t en secondes et RC la constante de temps (en secondes) du circuit.

  • Application numérique:  Prenons le même montage que précédemment avec C=1000µF, E=12V et R=2,2Kohm. On suppose le condensateur initialement déchargé, on a Vc(0)=0, Vc(infini) est la valeur de Vc une fois qu'il est chargé d'où Vc(infini)=12V et RC= 0,001 . 2200= 2,2 secondes (la constante de temps).
    On veut savoir en combien de temps Vc atteint la valeur 4V. On part de Vc(t) = Vc(infini) + [ Vc(0) - Vc(infini) ].exp(-t/RC)
    On met sous la forme    [ Vc(t) - Vc(infini) ] / [ Vc(0) - Vc(infini) ] = exp(-t/RC)
    On obtient t:  t = -RC.ln[( Vc(t) - Vc(infini) ) / ( Vc(0) - Vc(infini) )]
    Donc t = -2,2.ln(8/12) = 0.9 secondes
    
    
  • A quoi sert l'exercice précédent ?
    

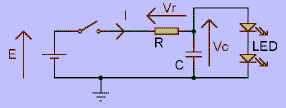
    Le schéma ci-contre est identique au précédent, la présence des LEDs permet de comprendre l'intérêt du condensateur. Les diodes utilisées sont de couleur verte (tension de seuil 2V), elles sont associées en série, il faut donc que Vc atteigne 4V pour qu'elles puissent briller. Par conséquent, tant que Vc est inférieur à 4V, le circuit se comporte de la même manière que sans les LEDs, puis Vc atteint 4V et les LEDs brillent.

            On a ainsi un retard créé par le condensateur; 0,9 secondes après avoir fermé l'inter, les LEDs s'illuminent.
    

  • Condensateur de liaison
    

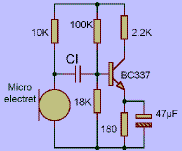
    On a vu que le condensateur a tendance à garder la tension à ses bornes constante. C'est cette caractéristique qui est mise à profit avec le condensateur de liaison (Cl). Il permet de transmettre les variations de tension d'un point à un autre, sans que ses points n'aient de tension moyenne commune. On trouvera aux bornes du condensateur la différence de ces tensions moyennes. Le condensateur laisse passer  le courant alternatif et il coupe le courant continu.

     

  • Association de condensateurs
    

    	En association série, la capacité équivalente aux deux condensateurs vaut : Ceq = (C1.C2)/(C1+C2)  On pose U = U1 + U2.    Pour une tension U donnée, U1 = U.C2/(C1+C2) et  U2= U.C1/(C1+C2) Remarque: Le condensateur formé de C1 et C2 peut accepter une tension max égale à U1max + U2max, en contre partie il a une capacité inférieure à celles de C1 et C2.
    	En parallèle, la capacité équivalente aux deux condensateurs vaut : Ceq = C1+C2 Remarque: La tension Umax est donnée par la plus petite tension U1max ou U2max
    	Cette association série est particulière  car elle consiste à mettre tête-bêche deux condensateurs électrolytiques. Elle est utilisée lorsque l'on a besoin de condensateurs de fortes capacités non polarisés. On peut réaliser cette association soi-même ou l'acheter toute faite. Remarque: Ce type de condensateur est utiliser dans les filtres (ex: pour séparer les voies dans une enceinte).

     

  • Impédance d'un condensateur
    L'impédance est une sorte de résistance, elle se mesure en ohm. L'impédance d'un condensateur est sa résistance en fonction de la fréquence.
    On définit ainsi  Z = 1 / ( w.C ) = 1 / (2.PI.f.C)    avec C la capacité du condensateur, f la fréquence en hertz (w est la pulsation en rad/s, w = 2.PI.f)  et Z l'impédance en ohm. (Voir les explications détaillées dans le complément)

• Complément

  • Ce graphique représente la charge d'un condensateur à courant constant. On a alors Vc = Q/C = (I.t)/C

   

  • Charge d'un condensateur

  On Reprend l'exemple de la charge d'un condensateur à travers une résistance

  	Pour t>=0, Vr + Vc = E, or Ic(t) = C.dVc/dt donc R.C.dVc/dt + Vc = E d'où l'équation différentielle: R.C.Vc' + Vc = E On a donc une solution de la forme: Vc(t) = A.exp(-t/RC) + B     Détermination de A et B: Vc(0)=0  D'où  A + B = 0 et Vc(infini) = E d'où B = E et donc A = -E  Par conséquent, Vc(t) = E - E.exp(-t/RC)
  	La charge du condensateur à travers une résistance est tracée ci-contre, on note certaines caractéristiques:   à  t= RC, Vc vaut 0,63.E   On peut considérer que Vc = E pour t>5.R.C   Enfin, la tangente à la courbe à t=0 coupe la droite V=E en t= R.C

  • Impédance d'un condensateur

    On veut calculer l'impédance d'un condensateur (Zc en ohm).  Zc = Vc/Ic  or  Ic = C.dVc/dt  d'où  Zc = Vc(t)/(C.Vc'(t)) Vc est une tension sinusoïdale de la forme: Vc(t) = E.sin(wt) donc Vc'(t) = E.w.cos(wt)   En négligeant le rapport de phase entre cosinus et sinus, on obtient:  Z = 1/(w.C)          ( En tenant compte du rapport de phase, on a en notation complexe:  Z = 1/( j.w.C) )

Remarque:   On peut utiliser la formule  Zc = 1/(w.C)  lors de la réalisation d'une alim sans transfo pour calculer la valeur du condensateur branché sur le signal alternatif.

• Avertissement:
  Toutes ces informations sont données a titre indicatif, et nous ne pourrons en aucun cas être tenus pour responsables en cas d'erreur.
  

Ecrivez nous: xizard@enib.fr et rbourdon@enib.fr